Overview of Markov Decision Process
MDP
a mathematical framework for modeling decision-making situations where outcomes are partly random and partly under the control of a decision-maker, characterized by states, actions, and rewards
Markov Property
- States in trading - market conditions
- Actions available - buying, selling, or holding a stock
- Reward structure - profit or loss resulting from the actions taken
Reinforcement Learning
Reinforcement derived from MDP Process
RL vs. Other Learning Paradigms
Pros:
- handles complex environments
- learns from delayed rewards
- adapts to dynamic markets
- balances exploration and exploitation
- scalable with deep learning
- provides robust decision-making
Cons:
- Requires extensive data
- High computational cost
- Difficult to tune hyperparameters
- Risk of overfitting
- Limited interpretability
- Insensitive to market changes
Q-Learning and Bellman Equation
Q-Learning
Q-Learning is a model-free reinforcement learning algorithm that enables an agent to learn the value of actions in a given state by using a Q-table Q-values: expected reward of taking a specific action when in a specific state Iteratively updated based on the Bellman equation and observed rewards
Bellman Equation
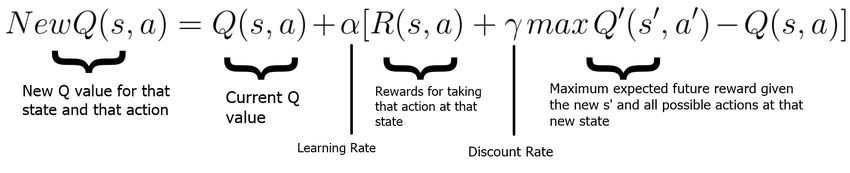
Discount Factor Gamma (
- determines the present value of future rewards
- higher discount factor encourages the agent to prioritize long-term rewards, and vice-versa
- want the Q-value to converge, discount factor plays an important role
State Transition Probabilities: only applies to defined environments with defined rules
Action Selection Strategies
Exploration: discover new actions and states Exploitation: taking actions that the agent already knows has high Q values to maximize the reward
Epsilon-Greedy Strategy: random actions for probability
- Epsilon decay factor can be linear or exponential
Other Strategies
- Boltzmann Exploration: Q-values and temperature
- Upper Confidence Bound
- Thompson Sampling
- Entropy-Based Exploration
- Exploration with Noise: Noisy Networks
Experience Buffer
Deep learning to approximate Q-value function allows to handle larger state spaces and more complex environments
Experience replay allows us to store pass experiences and sample during training to break correlation between consecutive experiences
- Makes data IID
Target Network: Copy weights to increase stability
Past ML Presentation
Decision tree ensembling
Drawing hyperplanes to separate the datapoints into clusters
Making decisions based on minimizing entropy - a measure of disorder or uncertainty
Random forest - using multiple weak classifiers to produce better predictive performance
https://github.com/RitvikKapila/TQT_ML_Workshop/blob/main/Chapter_12/Chapter_12_course.ipynb